How to Create Better Lerp Values
- Richard Bradley
- Jul 8, 2019
- 9 min read
Updated: Aug 1, 2019
Adding a fixed value every frame to a lerp value (0 to 1) is a functional way to achieve a lerp and in many cases may be exactly what you are looking for. However, when it comes to using lerp to move objects around your game world, the aforementioned method falls short on elegance.
Question: What do you mean by elegance, can numbers actually be elegant?
Answer: When the outcome of those numbers dictates what movement steps an object makes in your game world, then yes, numbers can be very elegant.
Adding a fixed value every frame to your lerp value will in turn move your object in fixed steps from its start position to a destination position. But what if you wanted the game object to gradually accelerate to its destination, or accelerate at the start and slow down when nearing it's destination? This cannot be achieved with simply adding a fixed value to your lerp value every frame, it will require a value that changes over time instead.
This is where this tutorial comes in, I will explain how you can use basic formulas to achieve this and hopefully give you a few ideas to take it further.
In order to understand the following sections you first need to understand the basics of Trigonometry, especially sine and cosine. So if its been a while since school, you might want to gem up before continuing.
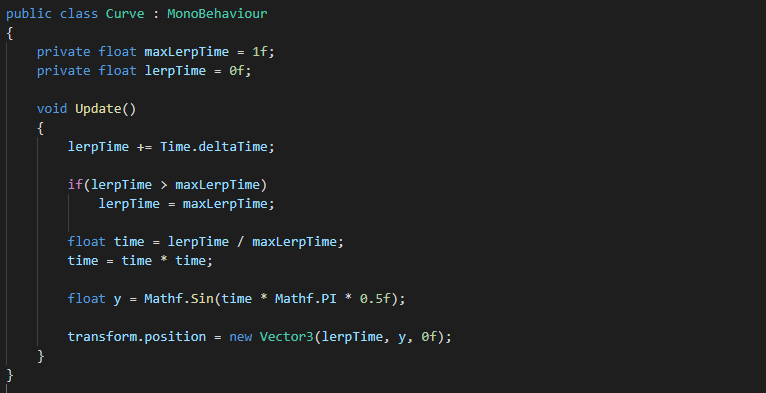
To help explain the lerp formulas I am going to take you through some code which uses sine to create a bell shaped plot of lerp values.
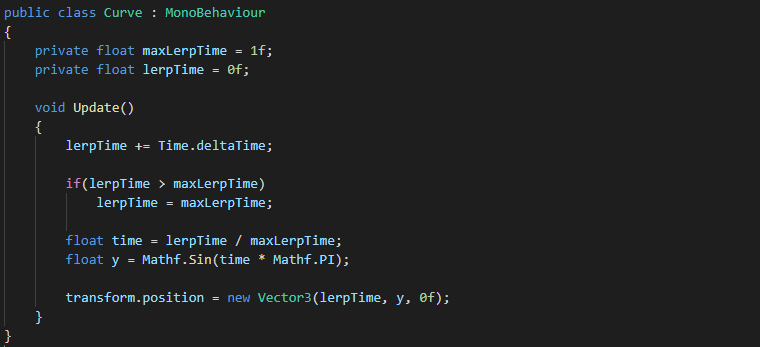
The first field, maxLerpTime, holds the maximum time we want the lerp to take, whilst the second field, lerpTime, stores the current lerp time passed.
The first line in the Update method adds Time.deltaTime to our lerpTime variable. This is how we add a time step to our lerpTime variable.
The if statement below simply checks whether the current lerpTime value is greater than our maxLerpTime value. If it is, we set our current lerpTime to equal the maxLerpTime value, as lerpTime should never be greater than the maximum lerp time allowed.
The first line of code below the if statement takes the current lerpTime, divides it by maxLerpTime then stores the result in a local variable name time (you should really test that maxLerpTime is greater than 0 before doing the division, I did not for simplicities sake). This time variable gives us a 0 to 1 value which describes the percent that lerpTime is of maxLerpTime. For example, if maxLerpTime was 4 and we incremented lerpTime by 1 every frame, then the following results would make up the percentage steps:
1 / 4 = 0.25 (25%)
2 / 4 = 0.50 (50%)
3 / 4 = 0.75 (75%)
4 / 4 = 1.00 (100%)
I chose the name time instead of say, percent, because in reality it is a percentage time step, but the main reason I chose this name is because it makes more sense in the context of the next line of code.
This line of code is where it all comes together. We create a float variable called y which will hold our object's y-position in world units (image we have a gameobject at position 0,0,0). This y variable stores a value from 0 to 1 which it receives from Mathf.Sin(time * Mathf.PI). As time increases, the resulting value gets closer to 3.141593 (Mathf.PI). As described on a unit circle, Pi is equivalent to half a circle, so as the resulting value gets closer to 3.141593 it effectively gets closer to completing a journey from one half of a circle to another. This journey starts off at 0 (right side of a half circle) peaking at 1 (top-middle of a half circle) and finishing at 0 again (left side of a half circle).
So basically Mathf.Sin(time * Mathf.PI) returns a value from 0 to 1 and back down to 0 again. This value is stored in our y variable and is used to move our object up and down.
The last line of code simply creates a new vector3 and updates it's x, y, z values ready to be used by transform.position, hence moving our object. For the x value we will use our lerpTime variable as it stores a (fairly) constant 0-1 (because maxLerpTime = 1) step increment. This should move our object across the x plane at a steady rate. With the y value we set it to equal our y variable, 0 to 1 and back to 0. This will move our object up and down in a half-circle motion. And finally, we set the z value to equal 0, because we do not want any movement on the z plane.
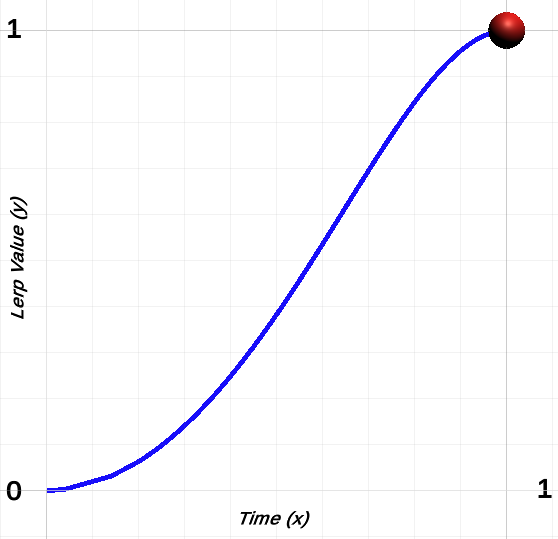
When the above code is placed on a gameobject (with a trail renderer attached) you will get the following outcome (I have added some text to better explain what's happening, but apart from that all motion graph shapshots are take directly from within Unity).

As you can see, the gameobject (red ball) moves in a bell shaped motion leaving a trail behind so we can map out its journey. Pretty cool huh?
Question: Yeah, its cool, I'll give you that. But how is this going to help me with elegant lerp values?
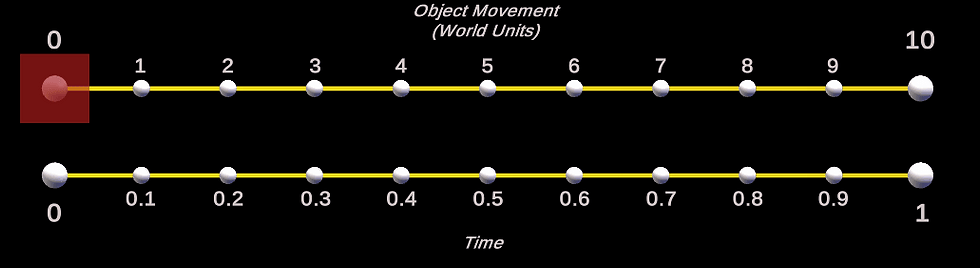
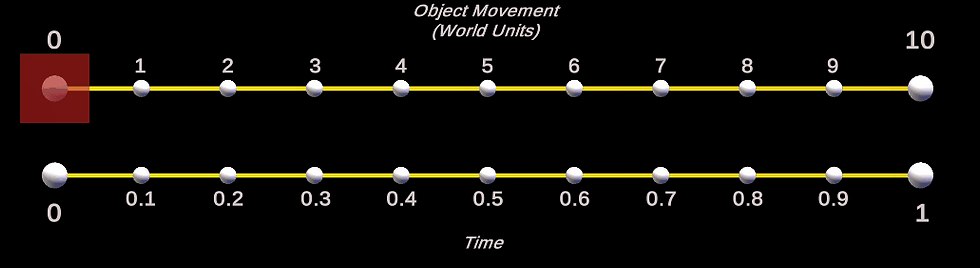
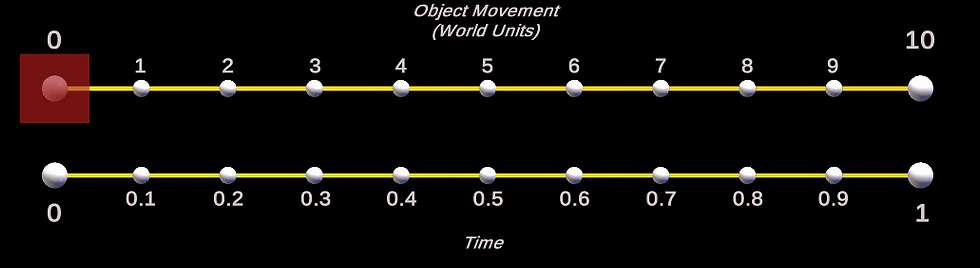
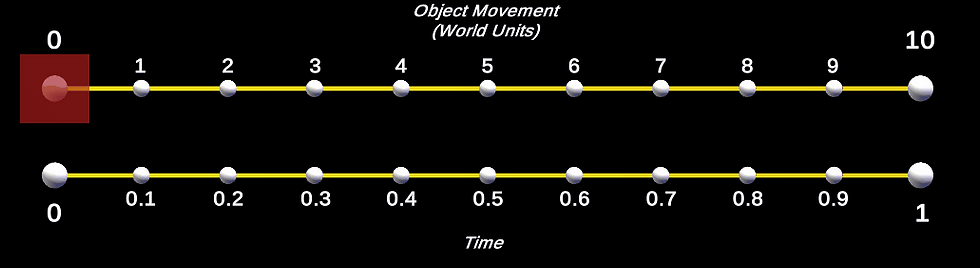
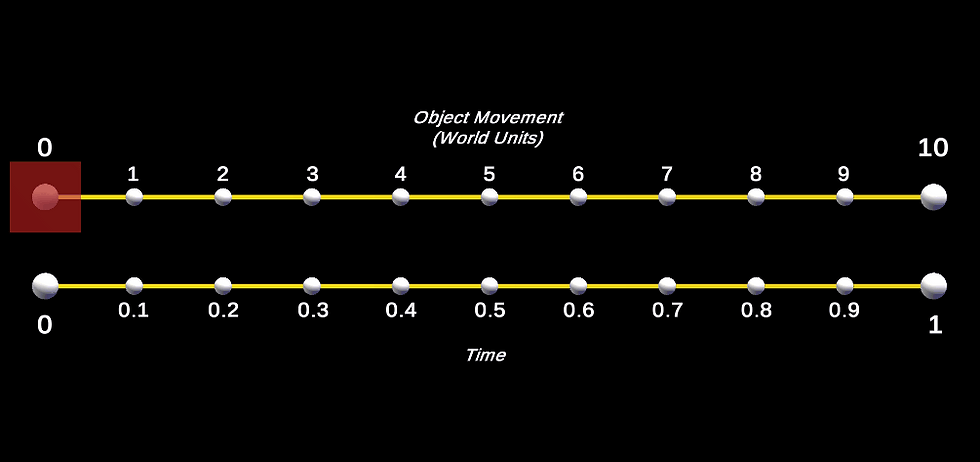
Answer: Well, take into account the shape from above and look at the actual movement of an object (red box below) from position 0,0,0 to 10,0,0 using the above lerp values.
(The true motion and shape is lost somewhat in GIF format, but is still noticeable).
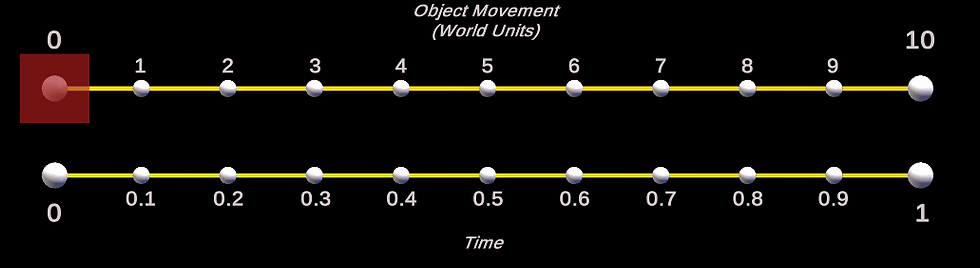
As you can see, it lerps from 0 (position 0,0,0) to 1 (position 10,0,0), then back down to 0 (position 0,0,0) again. You can see from the red box's motion that it follows the shape of the bell curve above.
Question: Ok, well I just want to go from 0 to 1, any cool ways of doing that?
Answer: Yep. Infact the whole previous example was building up to our first lerp motion formula.
Ease Out
When using sine we know that 6.283186 (Pi * 2) equates to a full circle. Therefore logic would suggest that if we halved 6.283186 we would end up with the value 3.141593 (Pi) which equates to a half circle (which we proved above). So by halving 3.141593 (Pi) we would end up with the value 1.5707965 (Pi/2) equating to a quarter circle.
When using a unit circle the following is true:
Sine(0) = 0
Sine(Pi/2) = 1
Sine(Pi) = 0
Sine(3*Pi/2) = -1
Sine(2*Pi) = 0
This is equivalent to:
Sine(0) = 0
Sine(1.570796) = 1
Sine(3.141593) = 0
Sine(4.712388) = -1
Sine(6.283186) = 0
As you can see sine(0) up to sine(1.5707965) will return a value between 0-1. Therefore, if we want our lerp value to be between 0 and 1, we will need to half Pi in our lerp formula.
Let's see this in code.
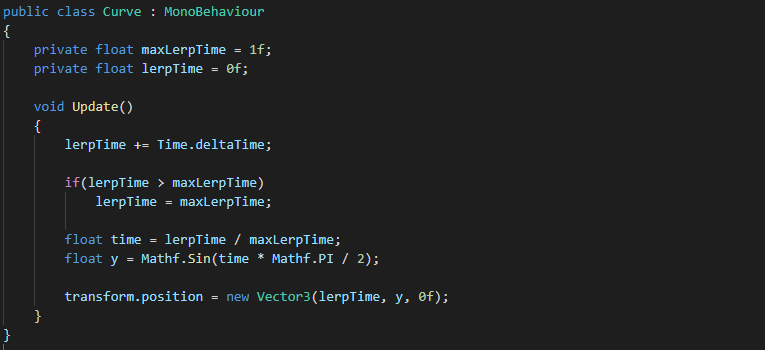
As you can see the only change from the bell shaped code is that we are now dividing Mathf.PI by 2, effectively clamping the Mathf.Sin return value between the values of 0-1.
Looking at the motion graph below you can clearly see that this has halved the bell shape. The reason for this is because we are not travelling a half circle anymore; we are now travelling one quarter of a circle.
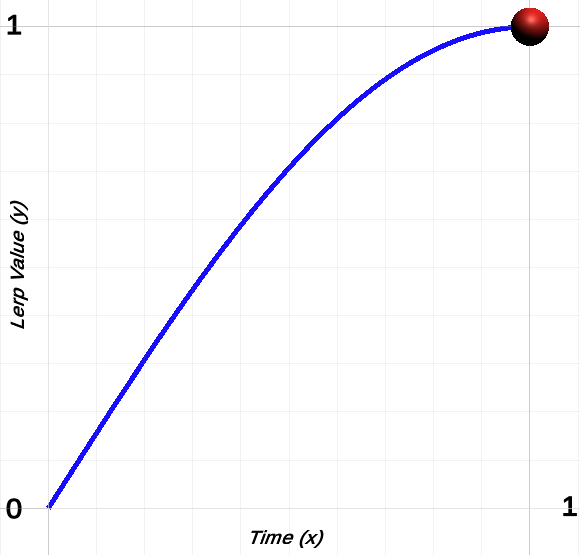
When the return value of this ease out formula is used within Vector3.Lerp, you get the following ease out motion.
There is one improvement I would like to make to our code before moving on to the ease in formula. At the moment we divide 3.141593 by 2, which is fine, but there is a slightly more performant way to do this.
Division in programming is less performant than addition, subtraction and multiplication. So, if we could use multiplication to halve Pi rather than division, then we would be saving on those precious resources.
Knowing that multiplying any value by 0.5 will return a result that is half the original value will benefit us, as we can now change the code to the following.
If you really wanted to take your optimisation to the extreme you could remove the multiplication by 0.5 and simply add a Pi value that has already been halved, like so:
float y = Mathf.Sin(time * 1.5707965f);
I stopped short of this kind of optimisation as it does not look user friendly. You can sometimes take optimisation to the extreme at the expense of readable code and if the optimisation really doesn't gain much in the way of performance, then you have a balancing act decision to make. Readability vs a slight performance increase.
Ease In
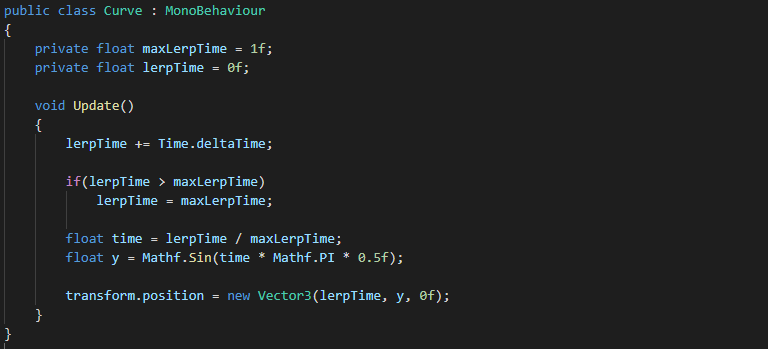
Question: Wow, cool. So I assume using cosine instead of sine will give us an ease in motion?
Answer: Not quite, let's see what happens when we replace Mathf.Sin with Mathf.Cos.
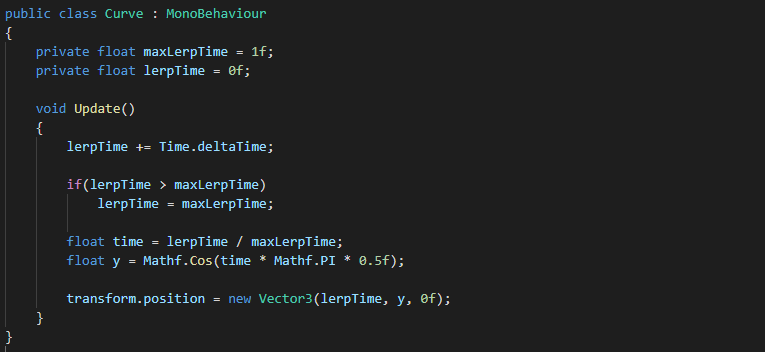
When this code is applied, you end up with the following shape:
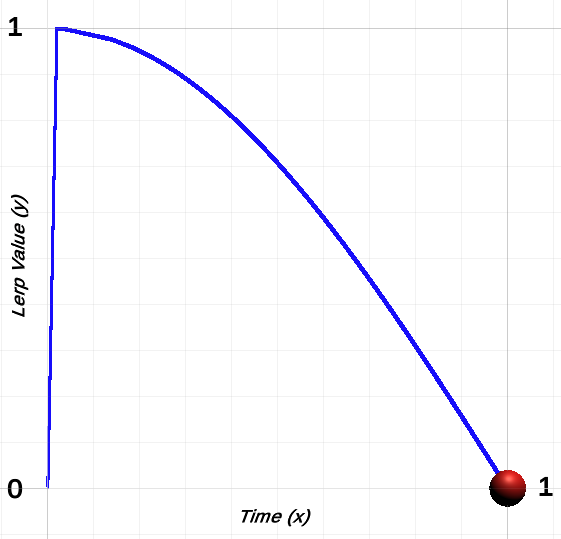
Thanks to the trail renderer, you can clearly see that the object jumps from 0 to 1 at the start and gradually curves down to 0. This of course is not what we want, as it would produce the following motion (which is certainly not an ease in motion).
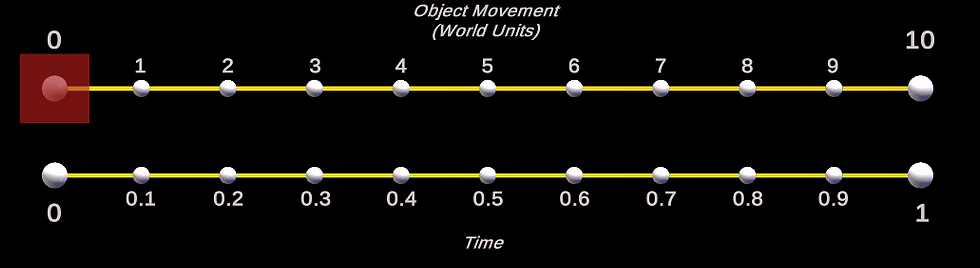
As you can see the red cube jumps to 10 and gradually lerps down to 0 world units on the x plane.
The reason for this is that cosine represents the adjacent ratio of the hypotenuse. In a unit circle, the hypotenuse is always 1, which is also true of cosine(0), as the adjacent will be at its greatest length possible. Sine represents the opposite ratio of the hypotenuse therefore sine(0) will be 0, because the opposite will be at its shortest length at this point in a unit circle.
More simply put, sine(0) starts at 0 while cosine(0) starts at 1. So if we amend our code to the following, we will have our ease in lerp formula.

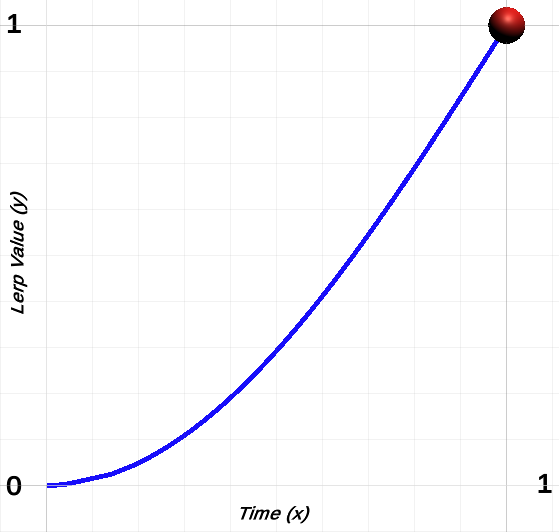
All we do is subtract the result of Mathf.Cos(time * Mathf.PI *0.5) from 1, hence giving us a value starting at 0 and ending at 1 (rather than the other way around).
Below is the motion graph for the above code.
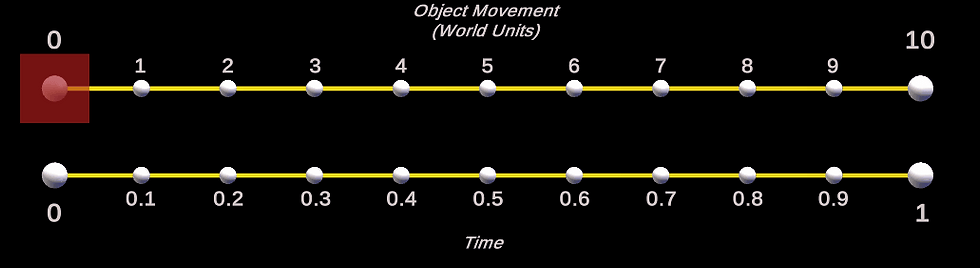
And here is the ease in lerp motion in all its glory.
Exponential
Question: Brilliant, any more?
Answer: Yep, next up exponential lerp.
Exponential growth is the idea that a value grows in relation to itself. Multiplying a value by itself (2 * 2 = 4) qualifies as exponential growth.
The following code uses this simple mathematical approach to achieve an exponential lerp.
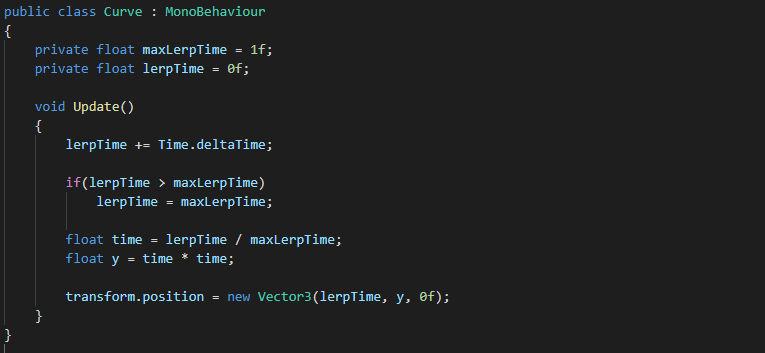
As you can see all we are doing now is multiplying time by time every Update loop, gone is the trigonometry.
The interesting thing is, multiplying any value between 0-1 by itself will in turn return a value between 0-1, no matter how many times you multiply them together.
Let's test this out, imagine that time increments by 0.2 per Update loop, starting at 0 and ending at 1.
First lets try time^2:
(0.0 * 0.0) = 0
(0.2 * 0.2) = 0.04
(0.4 * 0.4) = 0.16
(0.6 * 0.6) = 0.36
(0.8 * 0.8) = 0.64
(1.0 * 1.0) = 1.0
Now lets try time^4:
(0.0 * 0.0 * 0.0 * 0.0) = 0
(0.2 * 0.2 * 0.2 * 0.2) = 0.0016
(0.4 * 0.4 * 0.4 * 0.4) = 0.0256
(0.6 * 0.6 * 0.6 * 0.6) = 0.1296
(0.8 * 0.8 * 0.8 * 0.8) = 0.4096
(1.0 * 1.0 * 1.0 * 1.0) = 1.0
The following shows the motion graph for the code above.
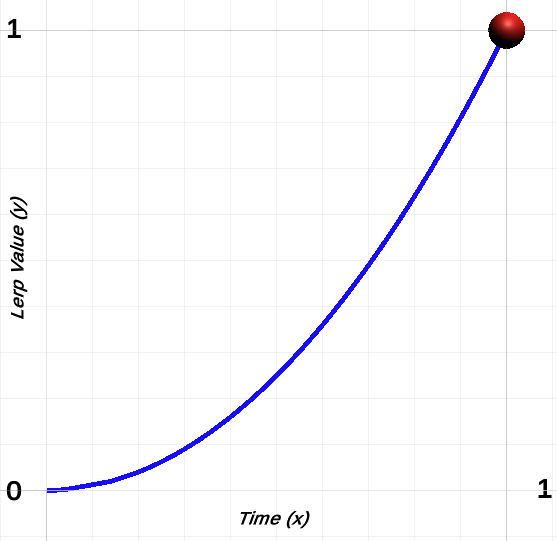
As you can see it starts off slow and gradually shoots up, better visualised by the gif below.
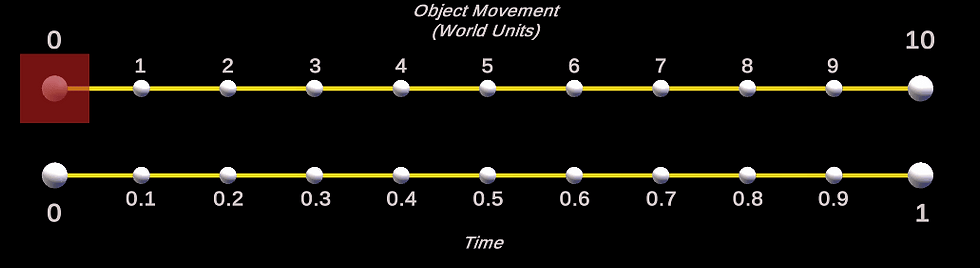
This code simply ups the ante by multiplying time by itself nine times.
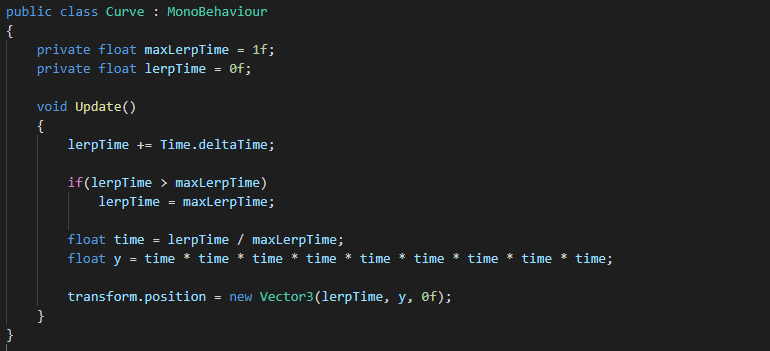
Here is the motion graph for the above code.
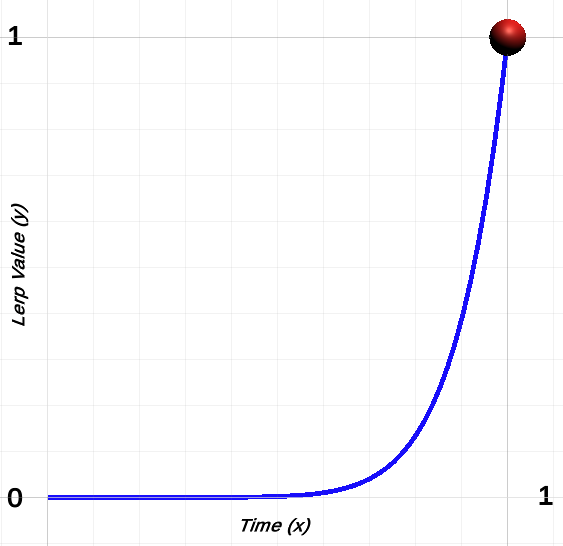
Better visualised by the following gif.
And there you have it, simple exponential growth.
Question: So could I combine exponential growth with say, ease out?
Answer: Let's give it a try.
The above code is the same code we used for ease out, except now we are feeding an exponentially grown time (time^2) into the Mathf.Sin method rather than a fixed (kind of, deltaTime is the time between the current and previous frame, which can vary) time step.
The following is the outcome on our motion graph.
With its lerp motion captured in the following gif.
This code sends time^4 or (time * time * time * time) into the Mathf.Sin method.

The following motion graph was plotted.

And its lerp motion has been captured below.
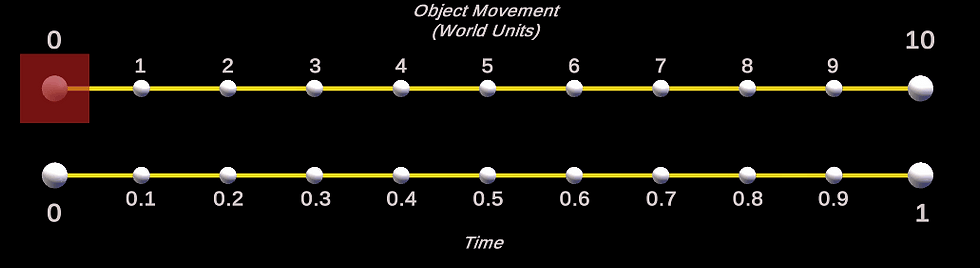
Smooth Step
Question: Brilliant, anything more?
Answer: Yes, I'm gonna sign off with smooth step.
Understanding the smooth step formula is not something I am going to cover in this tutorial (I have supplied a link in the related section at the bottom of this tutorial if you want to delve deeper). I will however show you the formula and a little shortcut thanks to the Unity API.
The following code implements the smooth step formula.
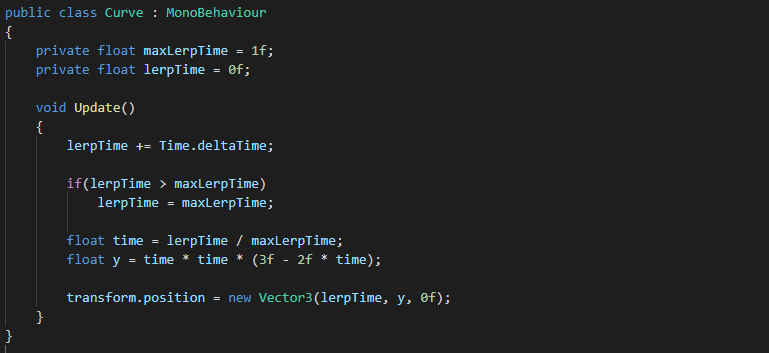
Below is the line of code which is our point of interest, as this is the smooth step formula in action.
float y = time * time * (3f - 2f * time)
Before showing you the motion graph for this formula, I wanted to show you another (easier?) way to achieve the same result by using Mathf.SmoothStep.
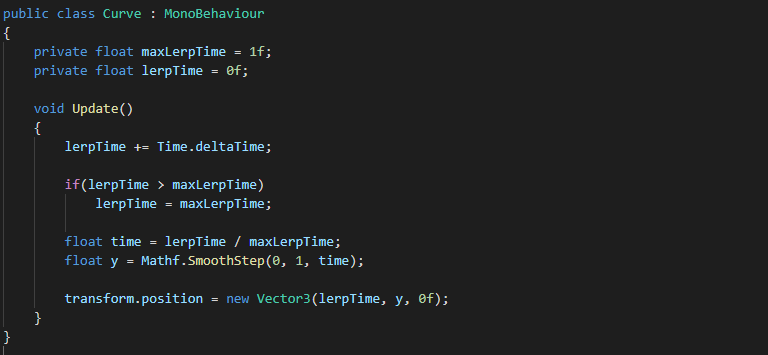
As you can see we have replaced the smooth step formula with Mathf.SmoothStep(0, 1, time). We are simply asking for a smooth step value between 0-1 over time.
Below is the motion graph I plotted using both smooth step implementation above.
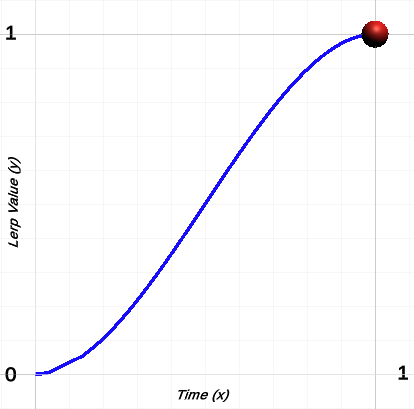
And the lerp motion for both for good measure.
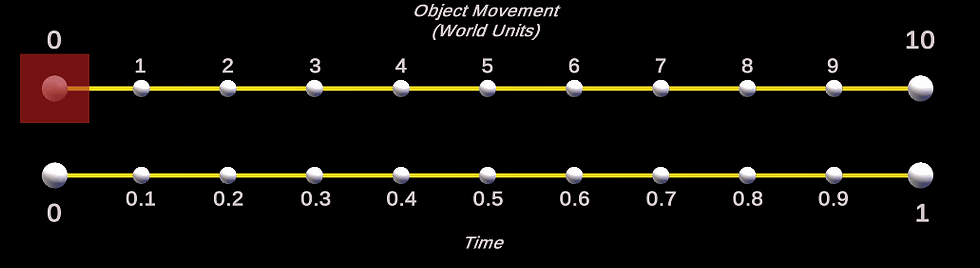
Both smooth step code snippets have the same outcome.
So there we have it, an easy way to achieve a smooth step lerp without having to understand a formula, yay.
If you like, try feeding an exponentially grown time value into the Mathf.SmoothStep(0, 1, time) method, see what happens (I have not tried this although I could guestimate the outcome).
Tweaking and fiddling about is a core part of learning, don't be afraid to experiment.
Until next time...
References
https://www.mathsisfun.com/exponent.html
https://www.mathsisfun.com/algebra/exponential-growth.html
https://www.mathsisfun.com/algebra/trigonometry.html
https://docs.unity3d.com/ScriptReference/Time-deltaTime.html
https://docs.unity3d.com/ScriptReference/Mathf.SmoothStep.html
https://docs.unity3d.com/ScriptReference/Mathf.html
https://chicounity3d.wordpress.com/2014/05/23/how-to-lerp-like-a-pro/
https://en.wikipedia.org/wiki/Smoothstep
Comments